Understanding sparse Merkle multiproofs
· Jim McDonald · 4 minutes read · 768 words ·Sparse Merkle multiproofs are an alternative to pollarding to provide space-efficient proofs for multiple values in the same Merkle tree. Merkle trees, proofs and pollards are explained in a previous article⧉ ; it is best to read and understand that prior to reading this article. For the remainder of this article the Merkle tree below will be used to explain multiproofs:
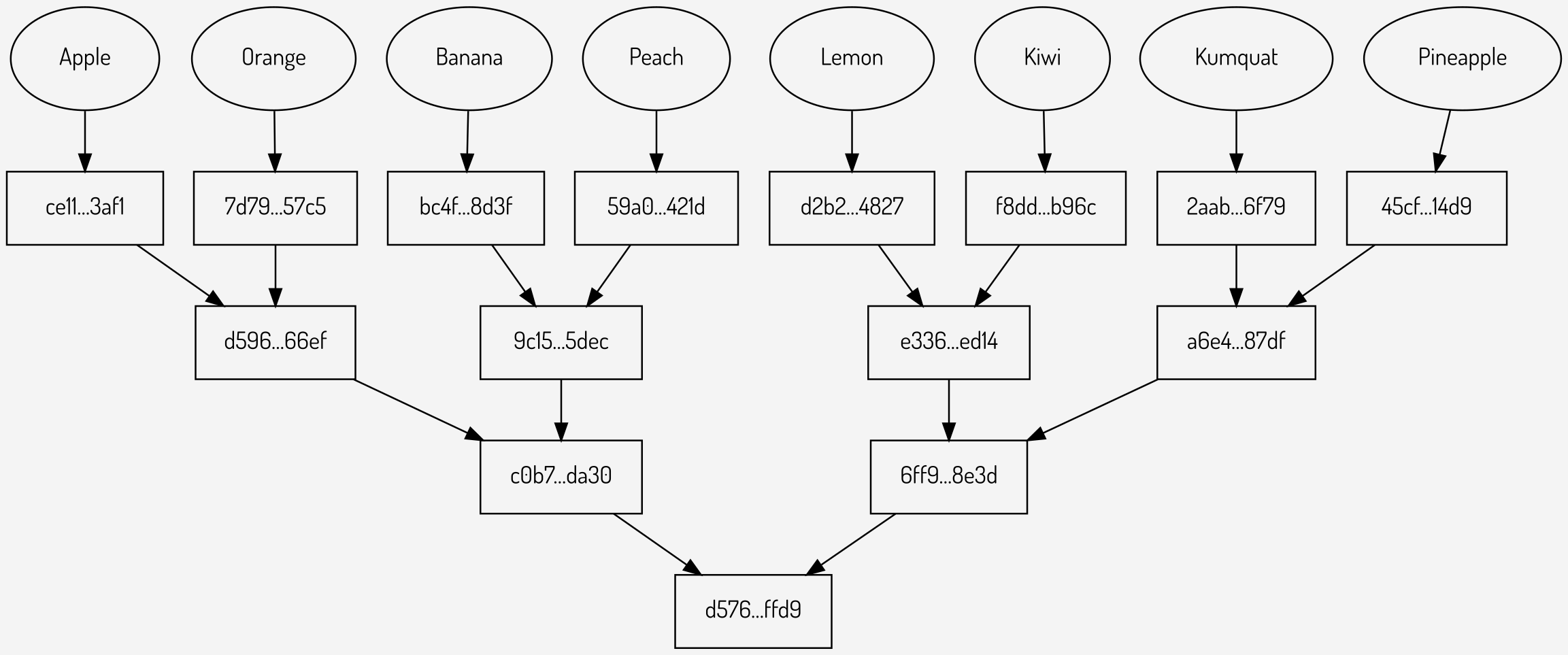
Figure 1: A Merkle tree
Sparse multiproofs were first proposed by Vitalik Buterin.
Multiproofs
A multiproof is simply a group of proofs against the same Merkle tree wrapped up together. The fact that they are together gives rise to the ability to make space savings. For example, below are three Merkle proofs against the above tree:

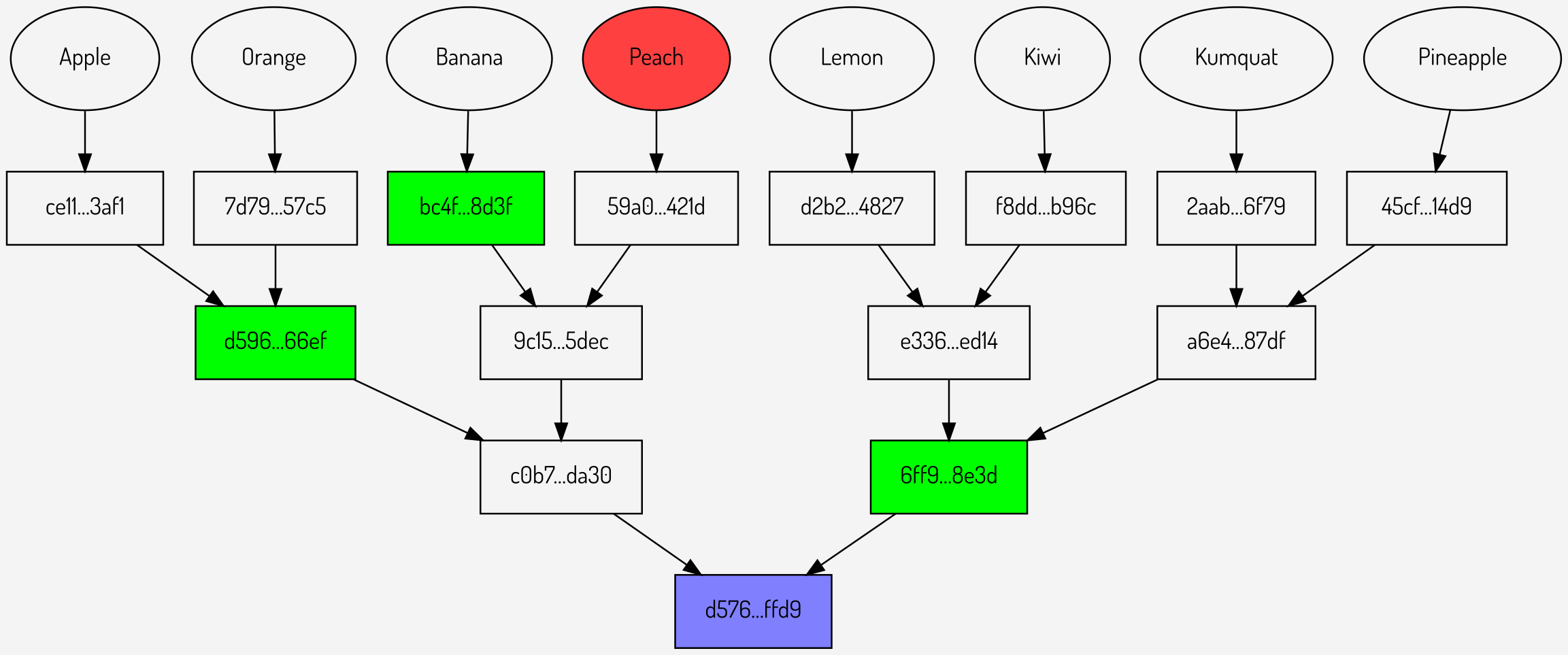
Figures
2,3,4: Individual Merkle proofs for Banana, Peach and Kumquat
It can be seen that these comprise of a total of 9 intermediate hashes (shown in green): 3 for each proof. Combining the individual proofs in to a multiproof gives the structure below:

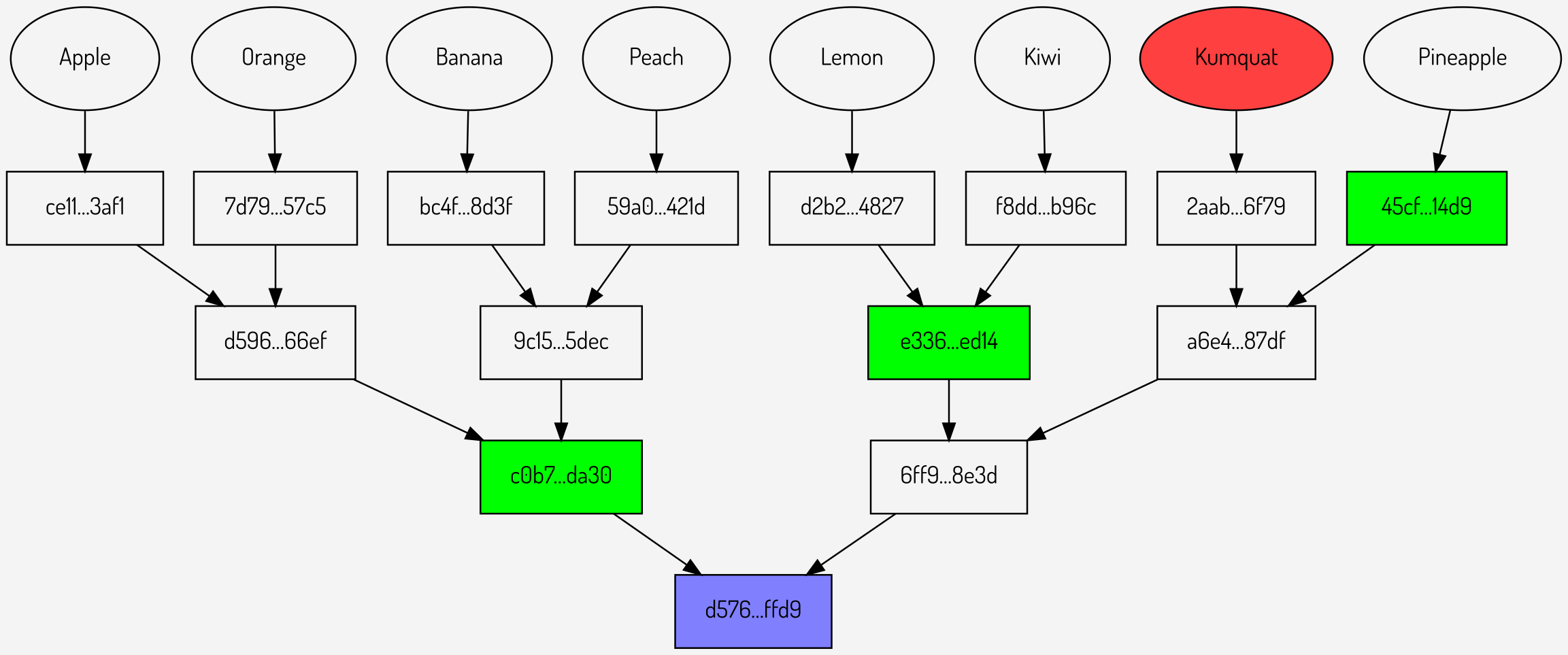
Figure
5: Merkle multiproof for Banana, Peach and Kumquat
The Merkle multiproof contains 7 intermediate hashes whereas the individual proofs contain 9 intermediate hashes, so a space saving has been achieved.
Sparse multiproofs
Although a Merkle multiproof does give some space saving it is possible to increase this saving by removing data that can be obtained through other means.
For example, taking the above Merkle multiproof there are a number of intermediate hashes that can be calculated. The hashes \(bc4F…8d3f\) and \(59a0…421d\) can be calculated by the verifier by hashing the values Banana and Peach, which are both known by the verifier. Looking closer towards the root the values \(c0b7…da30\) and \(6ff9…8e3d\) can also be calculated as both of their children (the hashes directly above them) are either supplied or can be calculated from the hashes above. These four nodes are shown in yellow below:
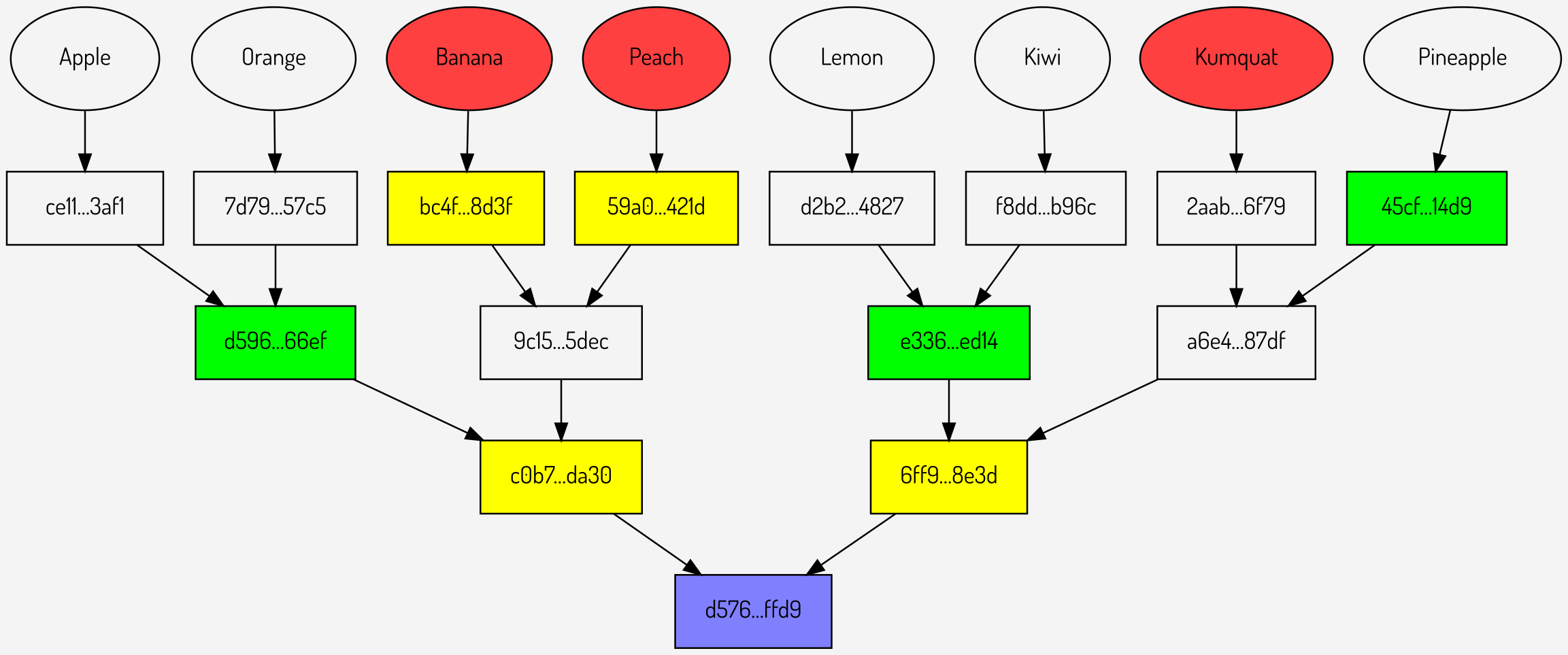
Figure 6: Merkle multiproof hashes that can be removed (shown in yellow)
Removing these values results in a sparse Merkle multiproof as shown below:
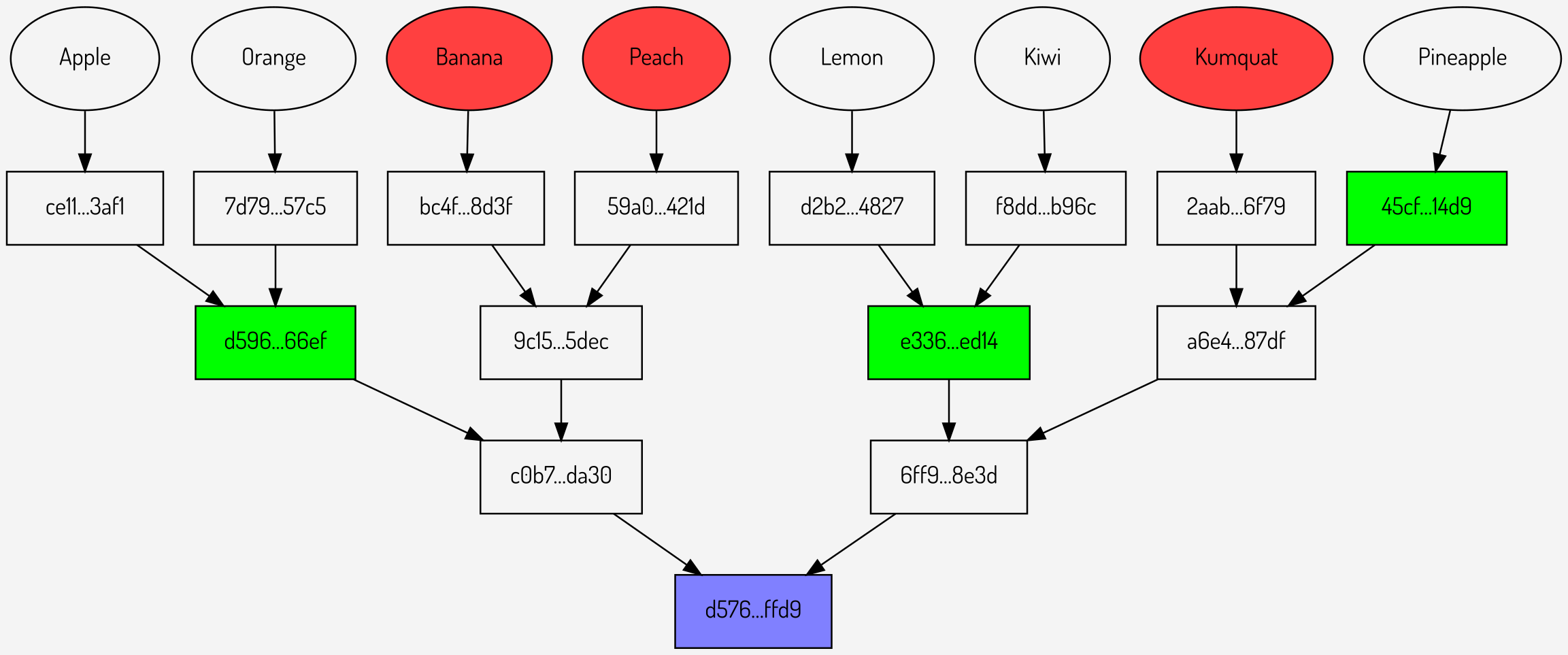
Figure 7: The final sparse Merkle multiproof
The sparse Merkle multiproof has reduced the number of hashes sent from an original 9 for individual proofs to just 3. It is also more efficient than pollarding, which would require 6 hashes to prove the same values.
To verify the values are part of the Merkle tree given the sparse multiproof the verifier would need to carry out the following steps (working from left to right and top to bottom):
- Hash
Bananato obtain \(bc4f…8d3f\) - Hash
Peachto obtain \(59a0…421d\) - Hash
Kumquatto obtain \(2aab…6f791\) - Hash \(bc4f…8d3f\) and \(59a0…421d\) to obtain \(9c15…5dec\)
- Hash \(2aab…6f79\) and \(45cf…14d9\) to obtain \(a6e4…87df\)
- Hash \(d596…66ef\) and \(9c15…5dec\) to obtain \(c0b7…da30\)
- Hash \(e336…ed14\) and \(a6e4…87df\) to obtain \(6ff9…8e3d\)
- Hash \(c0b7…da30\) and \(6ff9…8e3d\) to obtain \(d576…ffd9\)
at which point the final hash can be checked against the expected root to confirm that all values are in the tree.
A comparison of the space savings of Merkle pollards and sparse Merkle multiproofs over Merkle proofs is shown below for various numbers of values and proofs:
| Values | Proofs | Pollard saving | Multiproof saving (approx) |
|---|---|---|---|
| 1024 | 16 | 20% | 44% |
| 1024 | 32 | 29% | 55% |
| 1024 | 64 | 38% | 64% |
| 1024 | 128 | 48% | 75% |
| 4096 | 128 | 40% | 61% |
| 16384 | 128 | 34% | 50% |
| 65536 | 128 | 30% | 42% |
Note that the multiproof savings are approximate because they depend on the location of the particular values to be proven and hence how many intermediate hashes can be removed.
Comparison of sparse multiproofs and pollarding
Given that the above table shows that multiproofs provide space savings over pollarding why would one choose pollarding? Sparse Merkle multiproofs have different characteristics to Merkle pollards, specifically:
- they require all of the values and proofs to be present both at the time they are generated and at the time they are verified, whereas Merkle pollards allow proofs to be generated and verified individually
- they require more memory and CPU cycles to generate and verify than Merkle pollards
- they are harder to generate and verify in parallel than Merkle pollards
- they are variable size, whereas Merkle pollards generate fixed-size proofs for a given tree and total number of proofs
- it is possible for them to be larger than Merkle pollards in some situations due to the encoding system used to transmit the information; testing is advised
Ultimately it is down to the individual application’s requirements as which is more suitable. Both, however, provide significant savings over individual Merkle proofs and should be considered whenever multiple proofs against the same tree are required.
Sample implementation
An implementation of a Merkle tree with sparse multiproofs for the Go language can be found at https://github.com/wealdtech/go-merkletree⧉ .